Albedo
Albedo ( /ælˈbiːdoʊ/), or reflection coefficient, is the diffuse reflectivity or reflecting power of a surface. It is defined as the ratio of reflected radiation from the surface to incident radiation upon it. Being a dimensionless fraction, it may also be expressed as a percentage, and is measured on a scale from zero for no reflecting power of a perfectly black surface, to 1 for perfect reflection of a white surface.
Albedo depends on the frequency of the radiation. When quoted unqualified, it usually refers to some appropriate average across the spectrum of visible light. In general, the albedo depends on the directional distribution of incoming radiation. Exceptions are Lambertian surfaces, which scatter radiation in all directions according to a cosine function, so their albedo does not depend on the incident distribution. In practice, a bidirectional reflectance distribution function (BRDF) may be required to characterize the scattering properties of a surface accurately, although the albedo is a very useful first approximation.
The albedo is an important concept in climatology and astronomy, as well as in calculating reflectivity of surfaces in LEED sustainable rating systems for buildings, computer graphics and computer vision. The average overall albedo of Earth, its planetary albedo, is 30 to 35%, because of the covering by clouds, but varies widely locally across the surface, depending on the geological and environmental features.[1]
The term is derived from Latin albedo "whiteness", in turn from albus "white", and was introduced into optics by Johann Heinrich Lambert in his 1760 work Photometria.
Contents |
Terrestrial albedo
| Surface | Typical albedo |
|---|---|
| Fresh asphalt | 0.04[2] |
| Worn asphalt | 0.12[2] |
| Conifer forest (Summer) |
0.08,[3] 0.09 to 0.15[4] |
| Deciduous trees | 0.15 to 0.18[4] |
| Bare soil | 0.17[5] |
| Green grass | 0.25[5] |
| Desert sand | 0.40[6] |
| New concrete | 0.55[5] |
| Ocean Ice | 0.5–0.7[5] |
| Fresh snow | 0.80–0.90[5] |
Albedos of typical materials in visible light range from up to 0.9 for fresh snow, to about 0.04 for charcoal, one of the darkest substances. Deeply shadowed cavities can achieve an effective albedo approaching the zero of a black body. When seen from a distance, the ocean surface has a low albedo, as do most forests, while desert areas have some of the highest albedos among landforms. Most land areas are in an albedo range of 0.1 to 0.4.[7] The average albedo of the Earth is about 0.3.[8] This is far higher than for the ocean primarily because of the contribution of clouds.
Human activities have changed the albedo (via forest clearance and farming, for example) of various areas around the globe. However, quantification of this effect on the global scale is difficult.
The classic example of albedo effect is the snow-temperature feedback. If a snow-covered area warms and the snow melts, the albedo decreases, more sunlight is absorbed, and the temperature tends to increase. The converse is true: if snow forms, a cooling cycle happens. The intensity of the albedo effect depends on the size of the change in albedo and the amount of insolation; for this reason it can be potentially very large in the tropics.
The Earth's surface albedo is regularly estimated via Earth observation satellite sensors such as NASA's MODIS instruments on board the Terra and Aqua satellites. As the total amount of reflected radiation cannot be directly measured by satellite, a mathematical model of the BRDF is used to translate a sample set of satellite reflectance measurements into estimates of directional-hemispherical reflectance and bi-hemispherical reflectance. (e. g., .[9])
The Earth's average surface temperature due to its albedo and the greenhouse effect is currently about 15 °C. For the frozen (more reflective) planet the average temperature is below −40 °C[10] (If only all continents being completely covered by glaciers - the mean temperature is about 0 °C[11]). The simulation for (more absorptive) aquaplanet shows the average temperature close to 27 °C.[12]
White-sky and black-sky albedo
It has been shown that for many applications involving terrestrial albedo, the albedo at a particular solar zenith angle 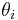 can reasonably be approximated by the proportionate sum of two terms: the directional-hemispherical reflectance at that solar zenith angle,
can reasonably be approximated by the proportionate sum of two terms: the directional-hemispherical reflectance at that solar zenith angle, 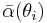 , and the bi-hemispherical reflectance,
, and the bi-hemispherical reflectance, 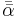 the proportion concerned being defined as the proportion of diffuse illumination
the proportion concerned being defined as the proportion of diffuse illumination 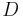 .
.
Albedo 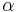 can then be given as:
can then be given as:
Directional-hemispherical reflectance is sometimes referred to as black-sky albedo and bi-hemispherical reflectance as white sky albedo. These terms are important because they allow the albedo to be calculated for any given illumination conditions from a knowledge of the intrinsic properties of the surface.[13]
Astronomical albedo
The albedos of planets, satellites and asteroids can be used to infer much about their properties. The study of albedos, their dependence on wavelength, lighting angle ("phase angle"), and variation in time comprises a major part of the astronomical field of photometry. For small and far objects that cannot be resolved by telescopes, much of what we know comes from the study of their albedos. For example, the absolute albedo can indicate the surface ice content of outer solar system objects, the variation of albedo with phase angle gives information about regolith properties, while unusually high radar albedo is indicative of high metallic content in asteroids.
Enceladus, a moon of Saturn, has one of the highest known albedos of any body in the Solar system, with 99% of EM radiation reflected. Another notable high-albedo body is Eris, with an albedo of 0.96 .[14] Many small objects in the outer solar system[15] and asteroid belt have low albedos down to about 0.05.[16] A typical comet nucleus has an albedo of 0.04.[17] Such a dark surface is thought to be indicative of a primitive and heavily space weathered surface containing some organic compounds.
The overall albedo of the Moon is around 0.12, but it is strongly directional and non-Lambertian, displaying also a strong opposition effect.[18] While such reflectance properties are different from those of any terrestrial terrains, they are typical of the regolith surfaces of airless solar system bodies.
Two common albedos that are used in astronomy are the (V-band) geometric albedo (measuring brightness when illumination comes from directly behind the observer) and the Bond albedo (measuring total proportion of electromagnetic energy reflected). Their values can differ significantly, which is a common source of confusion.
In detailed studies, the directional reflectance properties of astronomical bodies are often expressed in terms of the five Hapke parameters which semi-empirically describe the variation of albedo with phase angle, including a characterization of the opposition effect of regolith surfaces.
The correlation between astronomical (geometric) albedo, absolute magnitude and diameter is:[19] 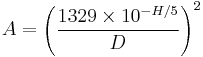 ,
,
where  is the astronomical albedo,
is the astronomical albedo,  is the diameter in kilometres, and H is the absolute magnitude.
is the diameter in kilometres, and H is the absolute magnitude.
Examples of terrestrial albedo effects
The tropics
Although the albedo-temperature effect is best known in colder regions on Earth, because more snow falls there, it is actually much stronger in tropical regions which receive consistently more sunlight.
Small-scale effects
Albedo works on a smaller scale, too. In sunlight, dark clothes absorb more heat and light-coloured clothes reflect it better, thus allowing some control over body temperature by exploiting the albedo effect of the colour of external clothing.[20]
Trees
Because trees tend to have a low albedo, removing forests would tend to increase albedo and thereby could produce localized climate cooling (ignoring the lost evaporative cooling effect of trees). Cloud feedbacks further complicate the issue. In seasonally snow-covered zones, winter albedos of treeless areas are 10% to 50% higher than nearby forested areas because snow does not cover the trees as readily. Deciduous trees have an albedo value of about 0.15 to 0.18 while coniferous trees have a value of about 0.09 to 0.15.[4]
Studies by the Hadley Centre have investigated the relative (generally warming) effect of albedo change and (cooling) effect of carbon sequestration on planting forests. They found that new forests in tropical and midlatitude areas tended to cool; new forests in high latitudes (e.g. Siberia) were neutral or perhaps warming.[21]
Snow
Snow albedos can be as high as 0.9; this, however, is for the ideal example: fresh deep snow over a featureless landscape. Over Antarctica they average a little more than 0.8. If a marginally snow-covered area warms, snow tends to melt, lowering the albedo, and hence leading to more snowmelt (the ice-albedo positive feedback). Cryoconite, powdery windblown dust containing soot, sometimes reduces albedo on glaciers and ice sheets.[22]
Water
Water reflects light very differently from typical terrestrial materials. The reflectivity of a water surface is calculated using the Fresnel equations (see graph).
At the scale of the wavelength of light even wavy water is always smooth so the light is reflected in a locally specular manner (not diffusely). The glint of light off water is a commonplace effect of this. At small angles of incident light, waviness results in reduced reflectivity because of the steepness of the reflectivity-vs.-incident-angle curve and a locally increased average incident angle.[23]
Although the reflectivity of water is very low at low and medium angles of incident light, it increases tremendously at high angles of incident light such as occur on the illuminated side of the Earth near the terminator (early morning, late afternoon and near the poles). However, as mentioned above, waviness causes an appreciable reduction. Since the light specularly reflected from water does not usually reach the viewer, water is usually considered to have a very low albedo in spite of its high reflectivity at high angles of incident light.
Note that white caps on waves look white (and have high albedo) because the water is foamed up, so there are many superimposed bubble surfaces which reflect, adding up their reflectivities. Fresh ‘black’ ice exhibits Fresnel reflection.
Clouds
Cloud albedo has substantial influence over atmospheric temperatures. Different types of clouds exhibit different reflectivity, theoretically ranging in albedo from a minimum of near 0 to a maximum approaching 0.8. "On any given day, about half of Earth is covered by clouds, which reflect more sunlight than land and water. Clouds keep Earth cool by reflecting sunlight, but they can also serve as blankets to trap warmth."[24]
Albedo and climate in some areas are affected by artificial clouds, such as those created by the contrails of heavy commercial airliner traffic.[25] A study following the burning of the Kuwaiti oil fields during Iraqi occupation showed that temperatures under the burning oil fires were as much as 10 °C colder than temperatures several miles away under clear skies.[26]
Aerosol effects
Aerosols (very fine particles/droplets in the atmosphere) have both direct and indirect effects on the Earth’s radiative balance. The direct (albedo) effect is generally to cool the planet; the indirect effect (the particles act as cloud condensation nuclei and thereby change cloud properties) is less certain.[27] As per [28] the effects are:
- Aerosol direct effect. Aerosols directly scatter and absorb radiation. The scattering of radiation causes atmospheric cooling, whereas absorption can cause atmospheric warming.
- Aerosol indirect effect. Aerosols modify the properties of clouds through a subset of the aerosol population called cloud condensation nuclei. Increased nuclei concentrations lead to increased cloud droplet number concentrations, which in turn leads to increased cloud albedo, increased light scattering and radiative cooling (first indirect effect), but also leads to reduced precipitation efficiency and increased lifetime of the cloud (second indirect effect).
Black carbon
Another albedo-related effect on the climate is from black carbon particles. The size of this effect is difficult to quantify: the Intergovernmental Panel on Climate Change estimates that the global mean radiative forcing for black carbon aerosols from fossil fuels is +0.2 W m−2, with a range +0.1 to +0.4 W m−2.[29]
Other types of albedo
Single scattering albedo is used to define scattering of electromagnetic waves on small particles. It depends on properties of the material (refractive index); the size of the particle or particles; and the wavelength of the incoming radiation.
See also
References
- ^ Environmental Encyclopedia, 3rd ed., Thompson Gale, 2003, ISBN 0-7876-5486-8
- ^ a b Pon, Brian (1999-06-30). "Pavement Albedo". Heat Island Group. http://eetd.lbl.gov/HeatIsland/Pavements/Albedo/. Retrieved 2007-08-27.
- ^ Alan K. Betts, John H. Ball (1997). "Albedo over the boreal forest". Journal of Geophysical 102 (D24): 28,901–28,910. Bibcode 1997JGR...10228901B. doi:10.1029/96JD03876. http://www.agu.org/pubs/crossref/1997/96JD03876.shtml. Retrieved 2007-08-27.
- ^ a b c "The Climate System". Manchester Metropolitan University. http://www.ace.mmu.ac.uk/Resources/gcc/1-3-3.html. Retrieved 2007-11-11.
- ^ a b c d e Tom Markvart, Luis CastaŁżer (2003). Practical Handbook of Photovoltaics: Fundamentals and Applications. Elsevier. ISBN 1-85617-390-9.
- ^ Tetzlaff, G. (1983). Albedo of the Sahara. pp. 60–63.
- ^ "Albedo - from Eric Weisstein's World of Physics". Scienceworld.wolfram.com. http://scienceworld.wolfram.com/physics/Albedo.html. Retrieved 2011-08-19.
- ^ Goode, P. R.; et al. (2001). "Earthshine Observations of the Earth’s Reflectance". Geophysical Research Letters 28 (9): 1671–1674. Bibcode 2001GeoRL..28.1671G. doi:10.1029/2000GL012580. http://www.agu.org/journals/ABS/2001/2000GL012580.shtml.
- ^ "MODIS BRDF/Albedo Product: Algorithm Theoretical Basis Document, Version 5.0". http://modis.gsfc.nasa.gov/data/atbd/atbd_mod09.pdf. Retrieved 2009-06-02.
- ^ "Snowball Earth: Ice thickness on the tropical ocean". http://www.atmos.washington.edu/~sgw/PAPERS/2002_Snowball.pdf. Retrieved 2009-09-20.
- ^ "Effect of land albedo, CO2, orography, and oceanic heat transport on extreme climates". http://www.clim-past.net/2/31/2006/cp-2-31-2006.pdf. Retrieved 2009-09-20.
- ^ "Global climate and ocean circulation on an aquaplanet ocean-atmosphere general circulation model". http://www.mpimet.mpg.de/fileadmin/staff/smithrobin/IC_JClim-final.pdf. Retrieved 2009-09-20.
- ^ Roman, M. O.; C.B. Schaaf, P. Lewis, F. Gao, G.P. Anderson, J.L. Privette, A.H. Strahler, C.E. Woodcock, and M. Barnsley (2010). "Assessing the Coupling between Surface Albedo derived from MODIS and the Fraction of Diffuse Skylight over Spatially-Characterized Landscapes". Remote Sensing of Environment 114: 738–760. doi:10.1016/j.rse.2009.11.014.
- ^ "Size, density, albedo and atmosphere limit of dwarf planet Eris from a stellar occultation". European Planetary Science Congress Abstracts 6. 2011. http://meetingorganizer.copernicus.org/EPSC-DPS2011/EPSC-DPS2011-137-8.pdf. Retrieved 2011-09-14.
- ^ Wm. Robert Johnston (2008-09-17). "TNO/Centaur diameters and albedos". Johnston's Archive. http://www.johnstonsarchive.net/astro/tnodiam.html. Retrieved 2008-10-17.
- ^ Wm. Robert Johnston (2003-06-28). "Asteroid albedos: graphs of data". Johnston's Archive. http://www.johnstonsarchive.net/astro/astalbedo.html. Retrieved 2008-06-16.
- ^ Robert Roy Britt (2001-11-29). "Comet Borrelly Puzzle: Darkest Object in the Solar System". Space.com. http://www.space.com/scienceastronomy/solarsystem/borrelly_dark_011129.html. Retrieved 2008-10-26.
- ^ Medkeff, Jeff (2002). "Lunar Albedo". Archived from the original on 23 May 2008. http://web.archive.org/web/20080523151225/http://jeff.medkeff.com/astro/lunar/obs_tech/albedo.htm. Retrieved 5 July 2010
- ^ Dan Bruton. "Conversion of Absolute Magnitude to Diameter for Minor Planets". Department of Physics & Astronomy (Stephen F. Austin State University). http://www.physics.sfasu.edu/astro/asteroids/sizemagnitude.html. Retrieved 2008-10-07.
- ^ "Health and Safety: Be Cool! (August 1997)". Ranknfile-ue.org. http://www.ranknfile-ue.org/h&s0897.html. Retrieved 2011-08-19.
- ^ Betts, Richard A. (2000). "Offset of the potential carbon sink from boreal forestation by decreases in surface albedo". Nature 408 (6809): 187–190. doi:10.1038/35041545. PMID 11089969.
- ^ "Changing Greenland - Melt Zone" page 3, of 4, article by Mark Jenkins in National Geographic June 2010, accessed July 8, 2010
- ^ http://vih.freeshell.org/pp/01-ONW-St.Petersburg/Fresnel.pdf
- ^ "Baffled Scientists Say Less Sunlight Reaching Earth". LiveScience. 2006-01-24. http://www.livescience.com/environment/060124_earth_albedo.html. Retrieved 2011-08-19.
- ^ http://facstaff.uww.edu/travisd/pdf/jetcontrailsrecentresearch.pdf
- ^ "The Kuwait oil fires as seen by Landsat". Adsabs.harvard.edu. 1991-05-30. http://adsabs.harvard.edu/abs/1992JGR....9714565C. Retrieved 2011-08-19.
- ^ "Climate Change 2001: The Scientific Basis". Grida.no. http://www.grida.no/climate/ipcc_tar/wg1/231.htm#671. Retrieved 2011-08-19.
- ^ Spracklen, D. V; Bonn, B.; Carslaw, K. S (2008). "Boreal forests, aerosols and the impacts on clouds and climate" (PDF). Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 366 (1885): 4613–4626. Bibcode 2008RSPTA.366.4613S. doi:10.1098/rsta.2008.0201. PMID 18826917. http://homepages.see.leeds.ac.uk/~eardvs/papers/spracklen08c.pdf.
- ^ "Climate Change 2001: The Scientific Basis". Grida.no. http://www.grida.no/climate/ipcc_tar/wg1/233.htm. Retrieved 2011-08-19.
External links
- Official Website of Albedo Project
- Global Albedo Project (Center for Clouds, Chemistry, and Climate)
- Albedo - Encyclopedia of Earth
- NASA MODIS BRDF/albedo product site
- Surface albedo derived from Meteosat observations
- A discussion of Lunar albedos